
1. 네트워크 플로우 문제
네트워크 플로우 문제는 네트워크 그래프에서 각 간선이 용량을 가지며, 한 정점(출발점)에서 다른 정점(도착점)으로 최대한 많은 유량을 보내는 문제입니다.

하나의 경로에서는 간선 중 가장 적은 용량이 최대 유량이 됩니다. 이때 유량이 시작되는 지점을 소스(Source), 유량이 도착하는 지점을 싱크(Sink)라고 합니다.
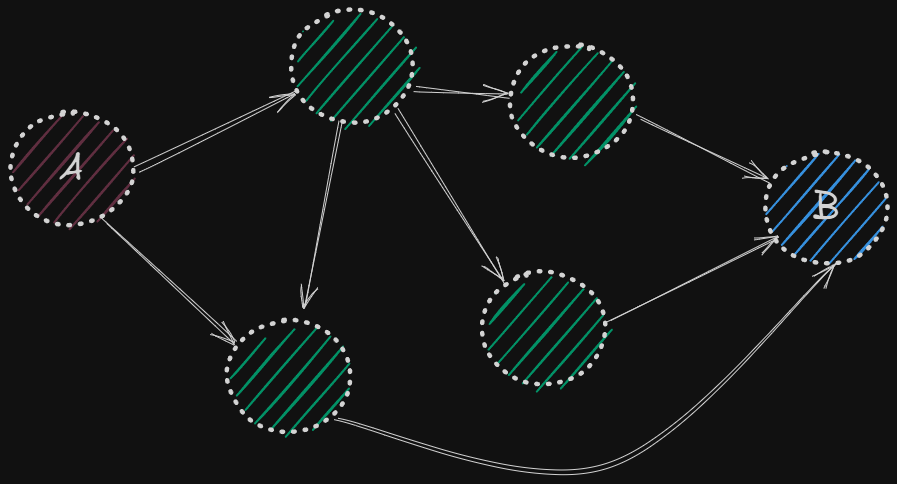
하지만 위와 같이 복잡한 네트워크에서는 A에서 B까지의 최대 유량을 구하는 것이 쉽지 않습니다. 다양한 경로와 잔여 용량을 고려해야 하기 때문입니다. 이를 해결하는 알고리즘이 포드-풀커슨, 에드몬드-카프 알고리즘입니다. 둘 다 원리는 같고 포드-풀커슨은 DFS, 에드몬드-카프는 BFS으로 그래프를 탐색합니다.
2. 에드몬드-카프 알고리즘(Edmonds-Karp Algorithm)
2.1. 작동 방식
에드몬드-카프 알고리즘은 증가 경로(Augmenting Path)를 반복적으로 찾고, 그 경로를 통해 유량을 보냅니다. 만약 증가 경로를 찾을 수 없다면 종료합니다.
증가 경로는 아래 두 조건을 만족하는 경로입니다.
- 소스에서 시작해서 싱크에 도달합니다.
- 경로 상의 모든 간선에 대해 (용량 - 현재유량) > 0 이어야 합니다.
한마디로 소스에서 싱크까지 가는 경로로, 경로 상의 모든 간선에 여유 용량(용량 - 현재 유량)이 0보다 큰 간선들이 존재하는 경로를 말합니다.

다음 그래프에서 S -> T까지의 최대 유량을 구해보겠습니다.

S -> A -> D -> T는 증가경로를 만족하므로 해당 경로를 통해 8만큼 유량이 흘러갑니다.

두번 째로, S -> A -> B -> T 증가경로를 통해 유량이 2만큼 흘러갑니다.

S -> C -> D -> T도 증가경로이므로 해당 경로를 업데이트합니다. 이때 더 이상 유량을 흘려보낼 남은 잔여 용량이 없으므로 증가경로는 존재하지 않고 종료 됩니다. 그러면 최종적으로, S에서 T로 가는 유량은 10 + 2 = 12 입니다. 하지만 이는 최대 유량이 아닙니다.

정답은 위와 같이 유량이 흐른 상태로, 10 + 4 = 14가 S -> T로 가는 최대 유량입니다. 즉, 증가경로를 탐색하는 순서에 따라 최대 유량을 구하는 정답이 될 수도 있고 안될 수도 있습니다.
그러면 어떻게 항상 최대유량을 구하도록 할 수 있을까요? 방법은 역방향 간선을 추가하는 것입니다.

역방향 간선은 네트워크에서 유량을 되돌릴 수 있는 논리적 간선으로, 유량이 흐르는 반대 방향을 나타냅니다. 위 그림을 예로, S -> C 경로에 2의 유량이 흘렀다면 역방향 간선(C -> S)은 -2가 흐르는 개념입니다.
정방향 간선 a ->b로 흐르는 유량을 f(a, b)라고 했을 때 다음의 특징이 있습니다.
- 역방향 간선 b -> a의 유량은 f(b, a)로 표시하며 f(b, a) + f(a, b) = 0입니다.
- 역방향 간선의 용량은 항상 0이며 이는 실제로 존재하지 않음을 나타냅니다.
- 역방향 간선에서 여유 용량은 정방향과 마찬가지로 (용량 - 현재유량)입니다. 따라서 역방향 간선에서 (용량 - 현재유량) > 0인 경우에 증가 경로의 간선이 될 수 있습니다.
역방향 간선은 유량이 실제로 반대로 흐르지는 않지만, 보낸 유량을 조정한다는 개념으로 생각하면 이해가 쉽습니다.
A -> D: 8/8
D -> A: -8/0
D -> A의 여유용량(용량 - 현재유량) = 0 -(-8) = 8
즉 D에서 A로 8의 유량을 보낼 수 있습니다. 여기서 만약 2의 유량을 보낸다면
D -> A의 유량: -8 + 2 = -6 이 되고 (정방향 유량 + 역방향 유량) = 0 이 되어야 하므로
A -> D의 유량: 8 - 2 = 6이됩니다.
정리하면 D -> A로 유량이 2가 흘렀다는 것은
A -> D로 흘러간 유량 중에서 -2만큼 조정되었다고 볼 수 있습니다.

역방향 간선을 추가하면, 기존의 경로에 반대 방향으로 유량을 되돌릴 수 있는 경로가 생깁니다. 이로 인해 새로운 증가 경로가 추가(파란색 경로) 되어, 유량을 더 보낼 수 있는 가능성이 생깁니다.( +2만큼)


에드몬드-카프 알고리즘의 시간 복잡도는 O(V ⋅ E²) 입니다. 이는 BFS가 각 증강 경로마다 실행되고, 최악의 경우 BFS가 V ⋅ E 번 실행될 수 있기 때문입니다. BFS는 각 실행 시 O(E) 시간이 걸리므로, 전체 시간 복잡도는 O(V ⋅ E²)가 됩니다.
2.2 코드
from collections import deque
def bfs(capacity, flow, source, sink, parent):
"""BFS를 이용해 경로를 찾습니다."""
visited = [False] * len(capacity)
queue = deque([source])
visited[source] = True
while queue:
current = queue.popleft()
for next_node in range(len(capacity)):
if not visited[next_node] and capacity[current][next_node] - flow[current][next_node] > 0:
queue.append(next_node)
visited[next_node] = True
parent[next_node] = current
if next_node == sink:
return True
return False
def edmonds_karp(capacity, source, sink):
"""에드몬드-카프 알고리즘으로 최대 유량을 계산합니다."""
n = len(capacity)
flow = [[0] * n for _ in range(n)]
parent = [-1] * n
max_flow = 0
while bfs(capacity, flow, source, sink, parent):
# 현재 경로의 최소 잔여 용량(유량)
path_flow = float('inf')
s = sink
while s != source:
path_flow = min(path_flow, capacity[parent[s]][s] - flow[parent[s]][s])
s = parent[s]
# 경로에 유량 추가
v = sink
while v != source:
u = parent[v]
flow[u][v] += path_flow
flow[v][u] -= path_flow
v = parent[v]
max_flow += path_flow
return max_flow
# 사용 예제
if __name__ == "__main__":
# 노드 수는 6이고, capacity[i][j]는 i에서 j로 가는 용량을 나타냅니다.
# S:0, A:1, B:2, C:3, D:4, T:5
capacity = [
[0, 10, 0, 5, 0, 0],
[0, 0, 4, 0, 8, 0],
[0, 0, 0, 0, 0, 10],
[0, 0, 0, 0, 4, 0],
[0, 0, 0, 0, 0, 10],
[0, 0, 0, 0, 0, 0]
]
source = 0 # 시작점
sink = 5 # 도착점
print("최대 유량:", edmonds_karp(capacity, source, sink))
- 문제
https://www.acmicpc.net/problem/6086
'컴퓨터 > 자료구조와 알고리즘' 카테고리의 다른 글
| 자료구조와 알고리즘 - 최소 신장트리(MST, Minimum Spanning Tree)와 크루스칼 알고리즘(Kruskal Algorithm) (0) | 2024.09.01 |
|---|---|
| 자료구조와 알고리즘 - 세그먼트 트리(Segment Tree) (0) | 2024.07.10 |
| 자료구조와 알고리즘 - BTree구조(B-Tree, B+Tree) (0) | 2024.05.09 |
| 자료구조와 알고리즘 - 벡터 검색 엔진 최적화 방법: HNSW(Hierarchical Navigable Small World Graphs) (0) | 2024.05.09 |
| 자료구조와 알고리즘 - 문자열검색 알고리즘(KMP) (0) | 2024.04.20 |

