
1. 브루트 포스 KNN(K-Nearest Neighbors) 방식
벡터 데이터를 이용한 유사도 검색은 이미지, 텍스트, 추천 시스템 등에서 활용되고 있습니다. 벡터 데이터베이스(Vector DB)는 이러한 유사도 검색을 위한 데이터베이스를 말하며, 주어진 쿼리 벡터와 가장 유사한 데이터 포인트를 찾는 데 사용됩니다.
유사도를 검색할 때 가장 단순한 방법은 모든 데이터를 탐색하는 것입니다. 이러한 방식을 보통 KNN이라고 합니다. KNN 알고리즘은 주어진 쿼리 벡터와 데이터베이스 내의 모든 벡터 간의 거리를 계산하여, 가장 가까운 K개의 이웃을 찾는 방식입니다.

벡터 DB에서 모든 데이터를 탐색하여 거리를 계산하는 방식은 가장 직관적이고 간단한 방법입니다. 이 방식을 흔히 "무차별 탐색(Brute Force Search)"이라고 부릅니다. 다음과 같은 장단점이 있습니다.
- 장점
1. 높은 정확도: 모든 데이터와의 거리를 계산하기 때문에, 가장 유사한 데이터 포인트를 정확하게 찾을 수 있습니다.
2. 단순성: 구현과 이해가 쉽습니다. 어떠한 특별한 데이터 구조나 복잡한 알고리즘이 필요하지 않습니다.
- 단점
1. 성능 저하: 데이터베이스 내의 모든 벡터와 거리를 계산해야 하므로 데이터가 많아질수록 계산 시간이 증가합니다.
2. 메모리 사용량: 모든 데이터를 메모리에 상주시켜야 하므로, 메모리 사용량이 많이 필요합니다.
2. ANN(Approximate Nearest Neighbor)
KNN(K-Nearest Neighbors, KNN) 방식은 대규모 데이터베이스에서 계산 복잡도와 메모리 사용량 등의 문제로 인해 한계를 가집니다. 이러한 한계를 극복하기 위해 개발된 것이 바로 근사 최근접 이웃(Approximate Nearest Neighbor, 이하 ANN) 알고리즘입니다.
ANN 알고리즘은 정확도를 약간 희생하면서도 훨씬 빠른 검색 속도를 제공합니다. 이는 대규모 데이터셋에서 유용합니다. ANN은 KNN의 주요 단점인 계산 성능을 해결하기 위해 다양한 최적화 기법을 적용합니다.
1) ANN의 종류
ANN를 구현한 방식은 여러가지가 있습니다. 이 중에 3가지만 간략하게 소개하겠습니다.

1. Locality-Sensitive Hashing (LSH): 유사한 벡터를 동일한 버킷에 할당하여 검색 시간을 단축하는 해싱 기법.
2. KD-Tree: 공간을 분할하여 데이터 포인트를 정렬하고 검색 시간을 단축하는 트리 기반 데이터 구조.
3. Hierarchical Navigable Small World (HNSW): 여러 계층의 그래프 구조를 활용하여 고차원 데이터의 유사도 검색 효율성을 높이는 알고리즘.
2) ANN의 장단점
ANN알고리즘에도 장단점이 있습니다.
- 장점
1. 빠른 검색 속도: ANN은 정확한 값을 찾는 대신, 근사 값을 빠르게 찾아냅니다.
2. 대용량 처리: 대용량 데이터셋에서도 효율적으로 작동할 수 있습니다.
- 단점
1. 정확성 일부 포기: ANN은 근사 값을 제공하기 때문에, 분석에 따라 유사도 검색의 정확도가 다소 떨어질 수 있습니다.
2. 복잡도 증가: ANN 알고리즘은 KNN에 비해 더 복잡한 데이터 구조와 알고리즘을 필요합니다.
3. 최적화 필요: ANN 알고리즘은 최적의 성능을 위해서 적절한 파라미터 설정이 필요합니다.
4. 메모리 사용량: 일부 ANN 알고리즘에서는 성능을 높이기 위해 더 많은 메모리를 필요 할 수 있습니다.
ANN 알고리즘 중에서 HNSW(Hierarchical Navigable Small World)에 대해서 알아 보겠습니다.
HNSW는 데이터 간의 가까운 이웃 관계를 계층적인 그래프 구조로 구성하는 방식입니다. 그래프의 각 노드는 데이터 포인트를 나타내며, 서로 유사한 포인트들 사이에 간선(edge)을 연결하여 탐색 공간을 줄여줍니다. 이러한 구조 덕분에 HNSW는 높은 차원의 데이터에서도 빠른 검색 성능을 보장합니다.
HNSW는 다음 두 개의 개념을 결합하여 응용한 것입니다.
- Small World Network
- Skip-List
3. Small World Network
1967년, 심리학자 스탠리 밀그램은 실험 참가자들한테 무작위로 선택된 대상에게 편지를 전달하는 실험을 진행했습니다. 참가자들은 대상을 아는 경우에 편지를 직접 전달할 수 있습니다. 만약 모른다면 그 대상을 알 것 같은 지인에게 편지를 보내야 했습니다. 대부분의 편지는 6단계 만에 최종 수신인에게 도달했으며, 이는 평균적으로 6명의 중간 단계를 통해 전 세계 누구와도 연결될 수 있음을 보여줍니다.
이 실험은 ' Small-World Network '라는 개념으로 이어졌습니다. Small-World Network는 소수의 연결을 통해 사회 전체가 밀접하게 연결되어 있는 구조를 설명합니다. 이러한 네트워크에서는 대부분의 노드(사람들)가 서로 가까운 거리에 있으며, 소수의 중간 연결만으로도 네트워크 전반에 걸쳐 빠르게 정보를 전달할 수 있습니다.
다시 한번 정리하면, Small-World Network는 네트워크 구조 개념으로, 노드들이 대부분 가까운 이웃들과 연결되어 있지만 몇몇 노드들이 먼 거리의 다른 노드들과도 연결되는 구조를 가지고 있습니다.

이러한 네트워크 구조는 짧은 평균 경로 길이와 높은 클러스터링 계수가 특징입니다.
- 짧은 평균 경로 길이의 의미
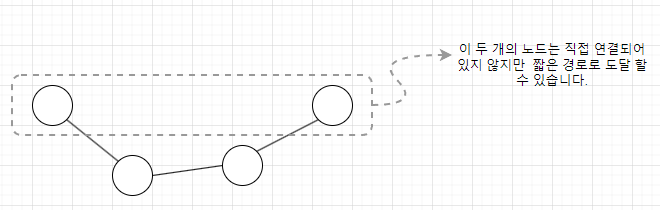
짧은 평균 경로 길이란 네트워크 안의 임의의 두 노드 간의 최단 경로 길이의 평균이 짧다는 것을 의미합니다. 예를 들어, 전 세계 사람들 사이의 관계를 나타내는 사회적 네트워크에서는 "여섯 다리 이론"처럼 몇 단계의 연결만으로도 누구에게나 접근할 수 있습니다. 이는 정보의 전파가 빨리 진행될 수 있는 현실세계를 반영한 것으로도 볼 수 있습니다.
- 높은 클러스터링 계수의 의미

높은 클러스터링 계수란 특정 노드의 이웃들이 서로 연결되어 있는 정도가 높다는 것을 의미합니다.예시로, 친구들끼리 서로 모두 알고 지내는 소규모 커뮤니티나 그룹 채팅방이 있습니다.
작은 세상 네트워크는 친구 관계망, 웹페이지 링크 구조, 연구 논문 공동 저자 네트워크에서 확인할 수 있습니다. 이러한 네트워크는 대부분의 노드들이 몇 단계 이내로 서로 연결될 수 있는 특징을 가집니다.
1) Watts-Strogatz 모델
Watts-Strogatz 모델은 작은 세상 네트워크를 구현하기 위한 모델입니다.
- 짧은 평균 경로 길이 (Short Average Path Length)
- 높은 클러스터링 (High Clustering)
Watts-Strogatz 모델은 위의 두 가지를 만족하는 네트워크 구조를 만들기 위해 다음의 단계를 따릅니다.
1. 초기 링 그래프

- 각 노드가 인접한 노드들과만 연결된 상태입니다.
- 클러스터링 계수는 높습니다. 즉, 각 노드의 이웃들끼리 잘 연결되어 있습니다.
- 하지만 평균 경로 길이가 깁니다. 임의의 두 노드 사이의 경로를 찾기 위해서는 여러 중간 노드를 거쳐야 합니다.
2. 랜덤 재배선 (Rewiring)

- 기존의 연결을 일부 랜덤하게 변경하여 먼 위치의 노드와 연결합니다.
- 이렇게 하면 짧은 경로가 유지되면서, 네트워크 전체의 클러스터링 계수는 크게 줄어들지 않습니다.
- 평균 경로 길이는 비약적으로 감소합니다. 이는 몇 개의 랜덤 연결로도 두 노드 사이를 빠르게 연결할 수 있게 합니다.
3. 랜덤 재배선 확률
Watts-Strogatz 모델에서 랜덤 재배선 확률(p)은 초기의 규칙적인 그래프(예: 정규격자형 네트워크)의 간선들을 임의로 재배선할 확률을 나타냅니다. p값에 따라 네트워크에 변화가 나타납니다.

1. p = 0
- 재배선 확률이 0이기 때문에 초기 링 형태를 그대로 유지합니다. 네트워크는 완전히 규칙적인 상태로 유지됩니다. 높은 클러스터링 계수를 가지고 있지만, 평균 경로 길이가 상대적으로 깁니다.
2. 0 < p < 1
- 네트워크가 점진적으로 무작위성을 띠기 시작합니다. 적당한 p값에서는 높은 클러스터링 계수를 유지하면서도 평균 경로 길이가 짧아지기 때문에, Small World Network 특성이 나타납니다.
3. p = 1
- 네트워크는 완전히 무작위 상태로 변합니다. 평균 경로 길이는 매우 짧아지지만, 클러스터링 계수가 현저히 낮아집니다.
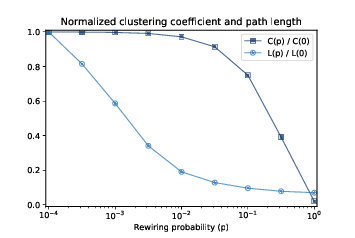
클러스터링 계수(C(p))와 평균 길이(L(p))는 p가 증가함에 따라 변합니다. 그래프를 보면 p가 증가함에 따라 클러스터링 계수는 서서히 감소하고 평균 길이는 급격하게 하락하는 것을 알 수 있습니다. 이를 통해 적절한 p 값을 선택하면 평균 길이를 낮게 유지하면서도 클러스터링 계수는 적절히 높게 유지할 수 있습니다. 이를 통해 Small-world network를 모델링 할 수 있게 되었습니다.
2) Navigable Small-World Network와 Kleinberg 모델
앞서 "스몰 월드 네트워크"의 개념과 이를 모델링하는 방법에 대해서 배웠습니다. 그러나 아직 해결해야 할 것이 있습니다.그것은 바로 효율적인 경로 탐색 방법을 찾는 것입니다.

예를 들어, 위의 네트워크에서는 노드 1에서 노드 3으로 가는 짧은 경로를 찾을 때 일반적인 그래프 탐색을 이용해서 찾을 수 있습니다. 하지만 이와 같이 모든 노드를 일일이 탐색하는 방식은 비효율적일 수 있습니다.
따라서 Small World Network의 특성과 함께 효율적인 경로 탐색를 가능하게 하는 것을 NSW(Navigable Small-world Network)라고 합니다. 이는 Kleinberg 모델을 통해 구현할 수 있으며 다음과 같은 특징을 가집니다
- 거리 기반 확률 모델: 노드 간의 연결 확률이 거리 함수에 따라 결정되어 가까운 거리의 노드는 더 자주 연결이 되고 먼 거리의 노드는 덜 연결됩니다.
- 그리디 라우팅: 각 노드는 자신과 직접 연결된 이웃 노드들에 대한 정보만 가지고, 목표 노드에 더 가까운 이웃을 선택하여 경로를 탐색합니다.
- 효율적인 경로 탐색: 네트워크 내에서 임의의 두 노드 간의 경로를 찾는 데 필요한 단계 수가 적습니다. 노드의 수가 n일 때 O(log n)의 시간복잡도를 가집니다.
- Kleinberg 모델
Kleinberg 모델은 효율적인 경로 탐색을 위한 토대를 마련하기 위해 다음과 같은 두 가지 주요 단계를 따릅니다
1. 그래프를 격자 위에 표시: 네트워크는 격자로 이루어진 평면에 노드로 표시됩니다.
2. 거리 기반 확률 분포: 각 노드는 다른 노드와 연결될 확률이 거리 기반으로 정해집니다. 구체적으로 노드(u)에서 노드(v )로 가는 확률은 두 노드의 맨해튼 거리(Manhattan Distance)의 역수입니다.

이는 거리가 멀수록 연결될 확률은 적어지고 거리가 가까울 수록 연결될 가능성이 높다는 것을 의미합니다.
이때 r은 연결확률을 조절하는 매개변수로 일반적으로 차원의 수만큼 설정하는 것이 최적임이 알려졌습니다. 즉, 2차원이면 r = 2입니다.
1. 격자무늬의 하얀색 노드에서 각 노드마다 연결하는 방식을 설명하겠습니다. 이때 격자무늬는 2차원이므로 r은 2입니다.

2. 하얀색 노드에서 맨허튼 거리가 1인 노드의 연결 확률은 1/(1**2) = 100%입니다.

3. 맨허튼 거리가 2인 노드들의 연결 확률은 1/(2**2) = 25%입니다.

4. 위처럼 맨허튼 거리를 기반으로 연결확률을 구해서 진행을 합니다.


Kleinberg 모델로 다음과 같은 그래프를 형성하고 하얀색 노드에서 파란색 노드로 가는 최적의 경로를 탐색하는 과정을 알아 보겠습니다.
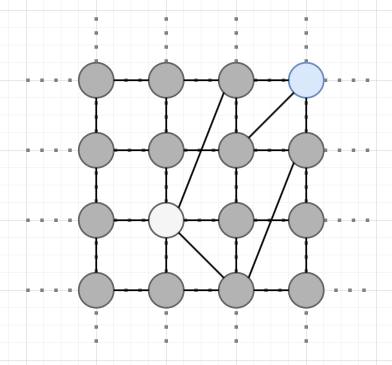
1. 하얀색 노드와 연결된 노드들 중에서, 도착지(파란색노드)와의 맨허튼 거리가 제일 짧은 노드로 이동합니다.

2. 1번과정을 반복하여 진행합니다.

3. 이 과정을 통해 최적의 경로를 구하였습니다. 이는 매 단계마다 최적의 방향을 선택하는 방식(그리디 라우팅)으로, 결과적으로 최적의 경로를 찾게 됩니다. 앞서 언급했듯이 이 방식은 평균적으로 O(log n)의 시간복잡도로 효율적인 경로 탐색을 제공합니다.

- 코드로 보면 다음과 같습니다.
def greedy_routing(start, end):
path = [start]
current = start #start에서 출발
while current != end: #end지점에 도착할 때 까지 반복
neighbors = graph[current] #현재 노드에서 연결된 노드들 확인
# end지점과 맨허튼 거리가 제일 작은 노드를 선택
current = min(neighbors, key=lambda n: manhattan_distance(n, end))
path.append(current)
return path
4. Skip-List

스킵 리스트는 정렬된 연결 리스트에서 데이터 검색/삽입/삭제를 O(log n) 시간 복잡도로 수행할 수 있는 선형 자료 구조입니다. 기존의 단일 연결 리스트에서 숫자 6에 접근하려면, 진입점부터 시작해 각 노드를 순차적으로 접근해야 하므로 시간 복잡도가 O(n)입니다.
스킵 리스트는 이러한 단점을 해결하기 위해 다중 레벨을 도입하여 더 빠르게 탐색할 수 있게 합니다. 스킵 리스트는 여러 레벨의 연결 리스트로 구성되어 있으며, 각 레벨은 하위 레벨의 노드를 건너뛸 수 있는 포인터를 포함합니다.
다음의 연산 과정을 거쳐서 진행됩니다.
num = 찾으려는 값
if num = 노드의 값 => 끝
elif num > 노드의 값 => 다음 노드로
elif num < 노드의 값 => 레벨 다운
1) 완전 스킵 리스트
그러면 어떤 기준으로 노드들이 다중 레벨을 지니도록 할까요? 단순한 방법으로는 2칸, 4칸, 8칸, 16칸 ...을 스킵하여 레벨을 올리는 방식이 있습니다.
- 기존 형태

- 두 칸 씩 띄어서 추가하기
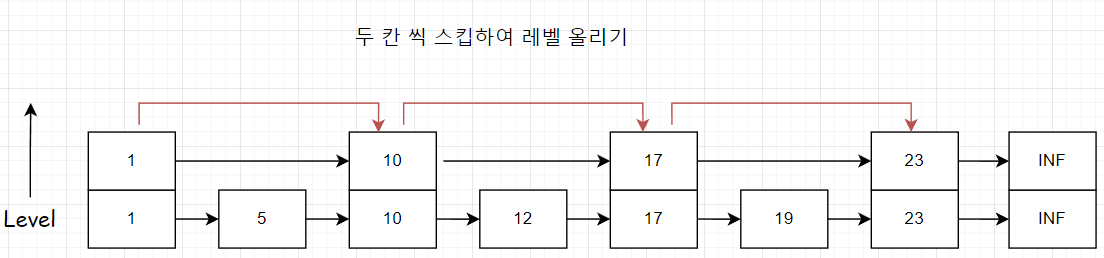
- 네 칸 씩 띄어서 추가하기

다음과 같이 레벨을 올릴 때 마다 2의 제곱 칸 씩 띄어서 레벨을 올리는 방식이 있습니다. 탐색 시간은 점점 n/2, n/4, n/8 ... 로 줄어들어서 O(log n)의 시간복잡도를 가집니다.
그러나 삽입과 삭제 연산은 여전히 n의 시간복잡도를 가집니다. 그 이유는 스킵 리스트를 재구성해야 하기 때문입니다.
예를 들어, [10, 15, 16, 17]의 리스트에 12를 삽입하면 [10, 12, 15, 16, 17]로 리스트가 재구성됩니다. 이 경우 모든 레벨에서 요소의 간격이 다시 계산되어야 합니다.
따라서 이러한 재구성 과정 때문에 삽입, 삭제 연산의 시간복잡도는 여전히 O(n)입니다. 모든 요소를 다시 재구성해야 하므로 효율성이 떨어집니다. 이러한 이유로 완전스킵리스트는 검색은 빠르지만, 삽입과 삭제 연산에서는 비효율적인 구조를 갖게 됩니다.
2) 랜덤 스킵리스트
완전 스킵리스트의 방식은 고정된 패턴으로 인해 유연성이 부족하고 특정 상황에서는 비효율적일 수 있습니다. 이를 해결하기 위한 방법이 랜덤 스킵리스트입니다. 랜덤 스킵리스트는 확률적 접근 방법을 통해 삽입 및 삭제 과정을 더욱 효율적으로 만들어줍니다.
랜덤 스킵리스트는 각 레벨의 노드가 확률적으로 결정되는 방식으로 구성됩니다. 예를 들어, 2 레벨에 노드를 배치할 확률이 1/2, 3 레벨에서는 1/4인 식으로 재귀적으로 적용됩니다. 이를 통해 삽입 및 삭제 과정에서도 평균적으로 O(log n)의 시간 복잡도를 유지할 수 있습니다.

- 레벨 1에서는 모든 노드가 존재하므로 확률이 1입니다.
- 레벨 2에서 노드를 가질 확률은 1/2입니다.
- 레벨 3에서 노드를 가질 확률은 1/4입니다.
- 레벨 k에서 노드를 가질 확률은 1/(2^(k-1))입니다.
이와 같은 확률 할당 방식은 노드가 상위 레벨로 갈수록 점점 더 적어지도록 만들며, 이를 통해 노드들의 탐색시간을 줄일 수 있습니다.
- 삽입 과정
1. 노드 레벨 결정: 새로 삽입할 노드의 레벨은 확률적 접근 방식으로 결정됩니다.
2. 삽입 위치 탐색: 현재 리스트에서 새 노드가 삽입될 위치를 탐색합니다.
3. 노드 삽입: 결정된 레벨에 따라 노드를 삽입합니다. 이때 기존 노드들의 포인터를 재설정하여 연결 구조를 유지합니다.
삽입할 노드의 레벨은 이미 1번에서 결정했기 때문에 스킵리스트를 재구성할 필요가 없어졌습니다. 이는 삭제 과정에서도 마찬가지입니다.
각 레벨이 무작위로 결정됨에 따라, 삽입 및 삭제 과정에서 최악의 경우를 고려한 시간 복잡도는 O(n)이지만, 평균적으로는 O(log n)의 시간 복잡도를 가집니다.
이는 대수 법칙(Law of Large Numbers)에 의해 n이 클수록 더욱 명확해집니다. 예를 들어, 동전을 던지는 실험을 무한히 반복하면, 결과적으로 앞면과 뒷면이 나타날 확률이 1/2씩 수렴하게 됩니다. 마찬가지로, 랜덤 스킵리스트에서도 n이 커질수록 각 레벨에서 노드가 존재할 확률은 정해진 값에 수렴하게 되며, 이는 전체 스킵리스트의 균형을 유지하게 됩니다.
5. HNSW(Hierarchical Navigable Small World)
이제, 앞에서 설명한 NSW, Skip-List 개념을 기반으로 HNSW를 설명할 차례입니다.
1) HNSW의 NSW
NSW는 Small-World Network 특성을 유지하면서 현재 위치에서 가장 가까운 이웃 노드로 이동하여 최단 경로를 찾을 수 있는 네트워크 구조를 말합니다. 여기서는 "Kleinberg 모델"을 직접 사용한 것은 아닙니다.
벡터 데이터를 사용하는 상황에서는 NSW를 다음의 과정을 통해 만듭니다.
- 벡터 데이터의 노드 정의: 각 벡터는 그래프의 노드로 간주됩니다.
- 유사도 기반 연결: 노드 간 연결은 유사도를 기반으로 합니다. 예를 들어, 유클리드 거리를 사용하여 벡터 간 거리를 계산하고, 가장 가까운 노드와 연결합니다.
- 매개변수 m: m은 각 노드가 연결할 수 있는 최대 이웃 수를 의미합니다. 이를 통해 그래프의 밀도,탐색의 효율성을 조절합니다.
다음은 m = 2의 경우에 NSW를 만드는 예시입니다.

https://towardsdatascience.com/whats-the-story-with-hnsw-d1402c37a44e
위의 출처에 따르면, 이 방법이 NSW의 일부를 만족한다고 언급합니다. Small-World Network의 특성에서 근처 노드들은 조밀하게 연결되고(높은 클러스터링 계수), 장거리 연결이 가끔씩 형성(짧은 평균경로길이)됩니다. 위 과정에서는 초기에 삽입된 벡터들이 무작위로 선택되어 멀리 떨어지기 때문에 소수의 장거리 연결을 형성하고, 새로 삽입된 벡터들은 근처의 벡터와 연결됩니다. 따라서 NSW에서 Small-World Network의 특성을 만족한다고 추론할 수 있습니다.
2) HNSW의 Skip-List
위 과정에서 구축한 NSW의 문제점을 보겠습니다.

쿼리 벡터 V와 네트워크 내 가장 가까운 노드를 탐색할 때, 해당 Entry 진입점에서 시작하여 그리디 탐색을 통해 가장 가까운 노드를 찾을 수 있습니다.
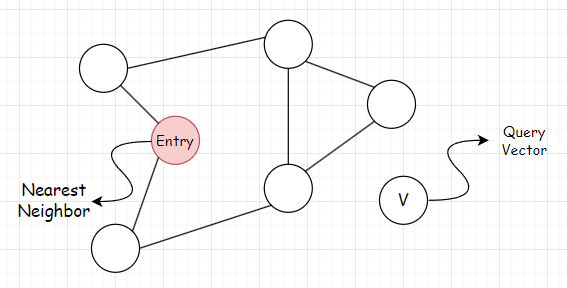
하지만 위의 진입점에서 출발하여 그리디 방식을 적용하면 가장 가까운 노드가 아닌 노드를 선택합니다. 이를 Local minimum 문제라고 합니다. 이를 해결하는 방법 중에 하나는 연결하는 링크 수(m)를 늘리는 것입니다. 하지만 이는 정확도가 높아지지만 그만큼 탐색 시간이 늘어나게 됩니다.
이 문제를 해결하기 위해서 계층 구조를 추가합니다.그 전에 Zoom-in 방식과 Zoom-out 방식을 알아야 합니다.
Zoom-out 방식은 크게 탐색하는 것을 말하고 Zoom-in은 세밀하게 탐색하는 것을 말합니다.

예를 들어 서점에서 원하는 주식 책을 찾는 과정을 보겠습니다.
- 줌 아웃 방식: 먼저 서점에서 경제 관련 책을 찾기 위해, 경제, 컴퓨터, 사회, 과학 등 전체 섹션 중에서 경제 섹션으로 이동합니다.
- 줌 인 방식: 경제 섹션에 도착한 후 더 구체적으로 주식, 금융, 부동산 등의 하위 주제들을 탐색합니다 여기서 주식 섹션으로 이동하여 주식 관련 책들을 살펴보고 자신에게 맞는 책을 선택합니다.
이 과정에서 처음에는 넓은 범위를 탐색하고, 이후 좁은 범위에서 세밀한 탐색을 통해 목표를 달성합니다.
이 개념을 계층에 적용하면 다음과 같습니다.

HNSW 알고리즘에서는 상위 계층에서 큰 범위로 탐색하는 줌 아웃 방식을 사용하고, 하위 계층으로 내려갈수록 더 세세한 탐색하는 줌 인 방식으로 진행합니다.
상위 계층에서는 노드의 수가 적고 덜 밀집된 연결을 가지며, 하위 계층으로 갈수록 노드 수가 많아지고 밀집도가 높아집니다. 이는 스킵 리스트의 개념을 적용한 것으로, 상위 레벨로 갈수록 노드의 밀도가 줄어들고 더 희소해지도록 설정합니다.
이러한 계층 구조를 통해 HNSW는 로컬 미니멈 문제를 완화하며 전체 탐색에서 O(log n)의 시간 복잡도를 보장할 수 있습니다.
3) HNSW 생성과정
HNSW 생성에는 다음의 파라미터들이 있습니다.
- m_max: 레벨 0을 제외한 모든 레벨에서 각 노드가 가질 수 있는 최대 연결 링크(이웃)의 수
- m_max0: 레벨 0에서 각 노드가 가질 수 있는 최대 연결 링크(이웃)의 수
- m_l: 레벨별로 연결할 확률을 조정하는 파라미터
- efconstruction: HNSW 생성에서 고려할 후보 군의 최대 벡터 수
- 지수 분포와 레벨별 삽입 확률
스킵 리스트에서 언급했듯이 상위레벨에서는 노드가 적고 하위레벨로 갈수록 노드가 더 많게 분포해야합니다. 이를 구현하기 위해서 지수분포를 사용합니다.

지수분포는 시간 간격이나 대기 시간과 같은 연속적인 사건 간의 간격을 모델링하는 데 사용되는 확률 분포입니다. HNSW에서는 지수 분포의 특성을 이용하여 레벨별 삽입 확률을 결정합니다.
지수분포의 그래프적인 특징을 보면 오른쪽으로 긴 꼬리를 보이는 형태입니다. 이를 이용하여 하위레벨 -> 상위레벨로 갈수록 노드의 개수가 점점 줄어들게 구현할 수 있습니다.
매개변수 λ(람다)에 의해 지수 분포의 그래프 모양이 결정됩니다. HNSW에서는 이 람다 값을 레벨별 연결 확률을 조정하는 파라미터 m_L로 설정합니다. 경험적으로 최적의 m_L 값은 1/log(m)으로 알려져 있습니다.
다음은 level = 5, m_l = 5 인 경우의 지수분포를 활용한 레벨별 삽입확률을 구한것입니다.

실제로는 0레벨에 배치할 확률이 높고, 상위 레벨로 갈수록 삽입 확률이 급격히 줄어들도록 계산합니다.
새로운 벡터가 들어오면, 위에서 레벨별로 계산한 삽입 확률(assign_probas)을 이용하여 어느 레벨에 삽입할지를 결정합니다. 이를 위해 무작위 숫자를 생성하고, 0레벨부터 출발하여 삽입 레벨을 결정합니다.
def random_level(assign_probas: list, rng):
# get random float from 'r'andom 'n'umber 'g'enerator
f = rng.uniform()
for level in range(len(assign_probas)):
# if the random float is less than level probability...
if f < assign_probas[level]:
# ... we assert at this level
return level
# otherwise subtract level probability and try again
f -= assign_probas[level]
# below happens with very low probability
return len(assign_probas) - 1
1. 확률 분포 설정
예시를 위해 assign_probas = [0.6, 0.3, 0.1]인 경우를 가정합니다. 이는 레벨 0에 삽입될 확률이 60%, 레벨 1에 삽입될 확률이 30%, 레벨 2에 삽입될 확률이 10%임을 의미합니다.
2. 무작위 숫자 생성
- 무작위 숫자 f가 0.45로 생성되었다고 가정합니다.
3. 레벨 결정 과정
- 레벨 0: f (0.45) < assign_probas[0] (0.6)이므로, 레벨 0에 삽입됩니다.
만약 f가 0.75였다면
- 레벨 0: f (0.75) > assign_probas[0] (0.6)이므로, f에서 0.6을 빼고 다음 레벨로 이동 (f = 0.15).
- 레벨 1: f (0.15) < assign_probas[1] (0.3)이므로, 레벨 1에 삽입됩니다.
- efconstruction
HNSW(Hierarchical Navigable Small World) 알고리즘에서 efconstruction은 노드를 삽입할 때 후보군의 탐색 범위를 조절하는 파라미터입니다. 이 파라미터는 초기에 1로 설정되며, 삽입할 레벨에 도달하면 원래 설정 값으로 확장됩니다.

1. 최상위 레벨에서 탐색 시작
- 삽입 과정은 최상위 레벨에서 시작하여, 그리디 방식으로 가장 가까운 노드를 찾아가며 하위 레벨로 이동합니다.
- 초기 efconstruction 값은 1로 설정됩니다. 따라서 유사도가 높은 1개의 노드만이 선택됩니다.
2. 삽입할 레벨에 도달
- 삽입할 레벨에 도달하면, efconstruction 값이 원래 설정 값(예: 5)으로 확장됩니다.
- 이 확장된 efconstruction 값은 더 많은 후보군을 고려하여 탐색 범위를 넓히는 역할을 합니다.
3. 후보군에서 연결할 노드 선택
- 예를 들어, m = 3이라면 가장 가까운 3개의 노드를 선택하여 연결합니다.
- 레벨 0에서는 m_max0을 사용하고, 그 외의 레벨에서는 m_max값을 사용합니다.
- FAISS에서는 기본적으로 m_max0 = m_max * 2로 설정하여, 0레벨에서 더 촘촘하게 연결되도록 합니다.
4. 레벨 0까지 반복
- 최초의 삽입 레벨에서 시작하여 레벨 0까지 내려가며, 각 레벨에서 링크를 연결하는 과정을 반복합니다.
4) HNSW 조회과정
HNSW(Hierarchical Navigable Small World) 알고리즘에서 efsearch는 탐색 시 후보군의 최대 수를 조절하는 파라미터입니다. efsearch 값이 높을수록 탐색범위가 넓어져서 정확도가 높아지지만, 그만큼 탐색 시간이 늘어납니다.

1. 최상위 계층에서 탐색 시작
- 탐색 과정은 최상위 계층에서 시작하여, 그리디 라우팅 방식으로 가장 가까운 노드를 찾아가며 하위 계층으로 이동합니다.
- 이 과정은 "Zoom-out" 과정으로, 넓은 범위에서 탐색을 시작하여 점점 좁혀가는 방식입니다.
2. Zoom-in 과정
- 하위 계층으로 이동하면서, 점점 더 정확한 후보군을 찾기 위해 세세한 탐색을 진행합니다.
- 이 과정에서 efsearch 값을 사용하여 탐색 범위를 넓힐 수 있습니다. efsearch 값이 높을수록 더 많은 후보군을 고려하여 탐색의 정확도를 높일 수 있습니다.
6. HNSW 파라미터 튜닝으로 최적화 방법
| 조회 속도 | 정확도 | 빌드 속도 | 메모리 사용량 | |
| m(링크 수) ↑ | 느려짐 | 좋아짐 | 느려짐 | 올라감 |
| efsearch(조회 탐색범위) ↑ | 느려짐 | 좋아짐 | - | - |
| efconstruction(구축 탐색범위) ↑ | - | 좋아짐 | 느려짐 | - |
(각 행마다 증가 했을 때의 관계)
HNSW (Hierarchical Navigable Small World) 알고리즘의 파라미터는 벡터 데이터의 특성과 사용 목적에 따라 달라질 수 있습니다. 따라서 튜닝을 통해 이를 조정할 필요가 있습니다.
이번 튜닝 작업에서는 정확도 지표로 재현율(Recall)을 설정하였습니다. 그 이유는 벡터와 일치하는 코사인 유사도를 기준으로, 모델이 얼마나 정답에 가깝게 예측했는지를 평가하기 위함입니다. HNSW로 검색된 벡터들이 브루트 포스 방식으로 조회 했을 때의 결과와 얼마나 잘 일치하는지를 측정합니다.
데이터는 약 18만 개의 데이터가 사용되었으며, 임베딩 모델로는 OpenAI의 1536차원의 "text-embedding-3-small" 모델을 사용합니다. 벡터 간 유사도는 코사인 유사도로 측정하고, 이에 대한 재현율을 기준으로 성능을 평가합니다. 튜닝에 사용할 데이터는 실제 1000개의 벡터 데이터를 이용합니다. 상위 유사도의 개수인 k = 20입니다.
또한 다음의 글을 보면 FAISS에서 차원(d)과 m(링크 수)에 따른 메모리 사용량 공식을 제시합니다.
Memory usage=(d×4+M×2×4) bytes per vector
https://www.youtube.com/watch?v=hCqF4tDPNBw&t=1723s
해당 영상에서 제시하는 튜닝 접근 전략으로 진행합니다.
1. m 파라미터: 수용가능한 수준의 메모리 사용량과 빌드 시간을 조정합니다.
2. efconstruction: efconstruction 값을 조정하여 수용할 수 있는 수준의 빌드 시간을 맞춥니다.
3. efsearch: 마지막으로, efsearch 값을 조정하여 조회 속도와 검색 정확도 간의 최적 타협점을 찾습니다.
1) m값 조정
M_values = [8, 16, 32, 64, 128, 256]
build_times = []
search_times = []
recalls = []
memory_usages = []
k = 20
# recall를 측정하기 위한 브루트포스 방식의 인덱스 생성
index_ground_truth = faiss.IndexFlatL2(d)
index_ground_truth.add(vectors)
#테스트 데이터
xq = vectors[:1000]
for M in M_values:
# HNSW 파라미터 설정
d = 1536 # 벡터 차원의 크기
index = faiss.IndexHNSWFlat(d, M)
print(f"M:{M}")
# 빌드 시간 결과
build_start = time.time()
index.add(vectors)
build_end = time.time()
build_times.append(round(build_end - build_start, 3))
print(f"build_time:{build_end - build_start}Sec")
# HNSW 결과
search_start = time.time()
D, I = index.search(xq, k=k)
search_end = time.time()
search_times.append(round(search_end - search_start, 3))
print(f"search_time:{search_end - search_start}Sec")
# 브루트포스로 조회한 결과
D_gt, I_gt = index_ground_truth.search(xq, k=k)
#재현율 결과
recall = recall_at_k(I, I_gt, k)
recalls.append(round(recall, 3))
print("Recall@{}: {:.4f}".format(k, recall))
#메모리 사용량
memory_per_vector = (d * 4 + M * 2 * 4) # 벡터 당 메모리 사용량 계산
total_memory_usage = round((memory_per_vector * index.ntotal) / 1024**3, 3) # 총 메모리 사용량 계산
memory_usages.append(total_memory_usage)
print(f"Total memory usage: {total_memory_usage}GB")
2) efconstruction값 조정
ef_construction_values = [50, 100, 150, 200, 250]
build_times = []
search_times = []
recalls = []
for ef_construction in ef_construction_values:
# HNSW 파라미터 설정
d = 1536 # 벡터 차원의 크기
M = 32 # 각 노드에 추가할 이웃의 수
index = faiss.IndexHNSWFlat(d, M)
index.hnsw.efConstruction = ef_construction
print(f"ef_construction:{ef_construction}")
#빌드 시간 결과
build_start = time.time()
index.add(vectors)
build_end = time.time()
build_times.append(round(build_end - build_start, 3))
print(f"build_time:{build_end - build_start}Sec")
# HNSW 결과
search_start = time.time()
D, I = index.search(xq, k=k)
search_end = time.time()
search_times.append(round(search_end - search_start, 3))
print(f"search_time:{search_end - search_start}Sec")
# 브루트포스로 조회한 결과
D_gt, I_gt = index_ground_truth.search(xq, k=k)
#재현율 결과
recall = recall_at_k(I, I_gt, k)
recalls.append(round(recall, 3))
print("Recall@{}: {:.4f}".format(k, recall))

3) efsearch값 조정
ef_search_values = [10, 15, 20, 25, 30]
build_times = []
search_times = []
recalls = []
for ef_search in ef_search_values:
# HNSW 파라미터 설정
d = 1536 # 벡터 차원의 크기
M = 32 # 각 노드에 추가할 이웃의 수
ef_construction = 50
index = faiss.IndexHNSWFlat(d, M)
index.hnsw.efConstruction = ef_construction
index.hnsw.efSearch = ef_search
print(f"ef_search:{ef_search}")
#빌드시간 결과
build_start = time.time()
index.add(vectors)
build_end = time.time()
build_times.append(round(build_end - build_start, 3))
print(f"build_time:{build_end - build_start}Sec")
# HNSW 결과
search_start = time.time()
D, I = index.search(xq, k=k)
search_end = time.time()
search_times.append(round(search_end - search_start, 3))
print(f"search_time:{search_end - search_start}Sec")
# 브루트포스로 조회한 결과
D_gt, I_gt = index_ground_truth.search(xq, k=k)
#재현율 결과
recall = recall_at_k(I, I_gt, k)
recalls.append(round(recall, 3))
print("Recall@{}: {:.4f}".format(k, recall))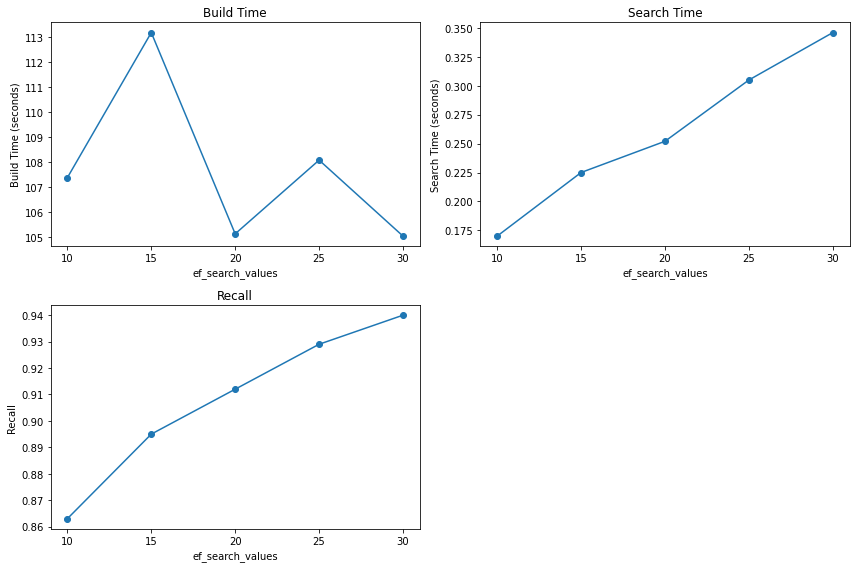
재현율 90%, 조회 속도를 0.2초대로 맞추기 위해, M을 32, efConstruction을 50, efSearch를 17로 설정한 HNSW의 결과입니다.(동시에 1000개의 쿼리 수행 시)

결과적으로 KNN 방식(브루트포스)에서 HNSW 방식으로 처리 시간을 1.6초에서 0.24초로 줄였으나, 정확도를 희생하여 재현율은 0.9에 이르렀습니다.
- 공부 출처들
https://chih-ling-hsu.github.io/2020/05/15/watts-strogatz#watts-strogatz-is-not-navigable
https://www.kth.se/social/upload/514c7450f276547cb33a1992/2-kleinberg.pdf
https://www.pinecone.io/learn/series/faiss/hnsw/
https://www.youtube.com/watch?v=mh09uZDQw4A&t=293s
https://ankitdash.hashnode.dev/hierarchical-navigable-small-worlds-algorithm-hnsw
https://towardsdatascience.com/whats-the-story-with-hnsw-d1402c37a44e
'컴퓨터 > 자료구조와 알고리즘' 카테고리의 다른 글
| 자료구조와 알고리즘 - 세그먼트 트리(Segment Tree) (0) | 2024.07.10 |
|---|---|
| 자료구조와 알고리즘 - BTree구조(B-Tree, B+Tree) (0) | 2024.05.09 |
| 자료구조와 알고리즘 - 문자열검색 알고리즘(KMP) (0) | 2024.04.20 |
| 자료구조와 알고리즘 - Trie (Prefix Tree) (0) | 2024.02.13 |
| 자료구조와 알고리즘 - 슬라이딩 윈도우(Sliding Window) (0) | 2024.01.02 |

