
1. 기본적인 문자열 검색 방법
text = "ababab"
pattern = "aba"

텍스트 "ababab"에서 "aba"의 패턴을 찾는 간단한 방법 중 하나는, 패턴을 텍스트의 각 위치에서 시작하여 순차적으로 비교하는 것입니다. 이 과정은 다음과 같이 진행됩니다:
1. 텍스트의 첫 번째 문자에서 시작하여, "aba"와 첫 세 문자 "aba"를 비교합니다. 이 경우, 패턴이 일치합니다.
2. 다음으로, 텍스트의 두 번째 문자로 이동하여, "aba"와 "bab"를 비교합니다. 이 경우, 패턴이 일치하지 않습니다.
3. 이후, 텍스트의 세 번째 문자로 이동하여, "aba"와 "aba"를 다시 비교합니다. 이 경우, 다시 패턴이 일치합니다.
4. 마지막으로, 텍스트의 네 번째 문자로 이동하여 "aba"와 "bab"를 비교합니다. 이 경우, 패턴이 일치하지 않습니다.
이 방식은 텍스트의 각 문자를 시작점으로 하여 패턴의 모든 문자를 차례대로 비교하는 방법입니다. 패턴이 일치하지 않으면, 비교 시작점을 텍스트에서 한 칸 옆으로 옮기고, 다시 패턴의 처음부터 비교를 시작합니다. 이 과정을 텍스트의 끝까지 반복하여, 패턴과 일치하는 모든 위치를 찾아냅니다.
이 방법은 구현이 간단하지만 시간복잡도가 O(n*m)입니다. 따라서 이는 패턴과 텍스트의 길이가 길다면 다소 비효율적인 방법입니다.(여기서 n은 텍스트의 길이이고, m은 패턴의 길이입니다.)
2. KMP 알고리즘
1) 부분 일치 테이블(Partial Match Table)
KMP(Knuth-Morris-Pratt) 알고리즘은 문자열 검색을 효율적으로 수행하기 위해 개발된 알고리즘입니다. 이를 알기 전에 부분 일치 테이블을 알아야 합니다.
부분 일치 테이블(Partial Match Table), 또는 파이(Pi)테이블은 KMP(Knuth-Morris-Pratt) 알고리즘에서 문자열 검색의 효율성을 높이기 위해 사용되는 중요한 구성 요소입니다. 이 테이블은 검색하고자 하는 패턴을 분석하여 생성되며, 패턴 내에서 접두사(prefix)와 접미사(suffix)가 일치하는 최대 길이를 각 위치별로 저장합니다.
예를 들어, 패턴 "ABCDABD"에 대한 파이 테이블은 다음과 같이 계산됩니다:
- A: 접두사와 접미사가 일치하는 부분이 없으므로 0
- AB: 접두사와 접미사가 일치하는 부분이 없으므로 0
- ABC: 접두사와 접미사가 일치하는 부분이 없으므로 0
- ABCD: 접두사와 접미사가 일치하는 부분이 없으므로 0
- ABCDA: 접두사 "A"와 접미사 "A"가 일치하므로 1
- ABCDAB: 접두사 "AB"와 접미사 "AB"가 일치하므로 2
- ABCDABD: 접두사와 접미사가 일치하는 부분이 없으므로 0
최종적으로 파이 테이블은 [0, 0, 0, 0, 1, 2, 0] 입니다.
파이테이블을 구하는 구체적인 방법은 다음과 같습니다.

- 코드
def compute_pi(pattern):
n = len(pattern)
pi = [0] * n # 접두사 테이블 초기화
j = 0 # 접두사의 길이
# i는 1부터 문자열의 끝까지 반복
for i in range(1, n):
# j > 0이고 현재 문자가 접두사의 다음 문자와 일치하지 않는 경우
while j > 0 and pattern[i] != pattern[j]:
j = pi[j - 1] # j를 감소시키면서 일치하는 위치를 찾음 => 그다음 접두사,접미사 부분을 확인
# 현재 문자가 접두사의 다음 문자와 일치하는 경우
if pattern[i] == pattern[j]:
j += 1 # 접두사 길이를 증가
pi[i] = j # 해당 위치에 접두사 길이를 저장
return pi
2) KMP 알고리즘의 기본 원리
처음에 언급한 방식은 패턴의 불일치가 발생할 때마다 검색 시작 위치를 한 칸씩 이동시키고, 패턴의 처음부터 다시 비교를 시작합니다. 이는 특히 패턴과 텍스트가 길고, 패턴 내에 반복되는 문자열이 많을 경우 많은 중복 비교를 발생시키며 비효율적입니다.
KMP 알고리즘은 이러한 비효율성을 개선하기 위해 파이 테이블을 사용합니다. 불일치가 발생했을 때, 이미 일치했던 부분의 접두사와 접미사 정보를 활용하여 패턴을 건너뛰므로, 검색 시간을 단축하고 효율을 높일 수 있습니다.
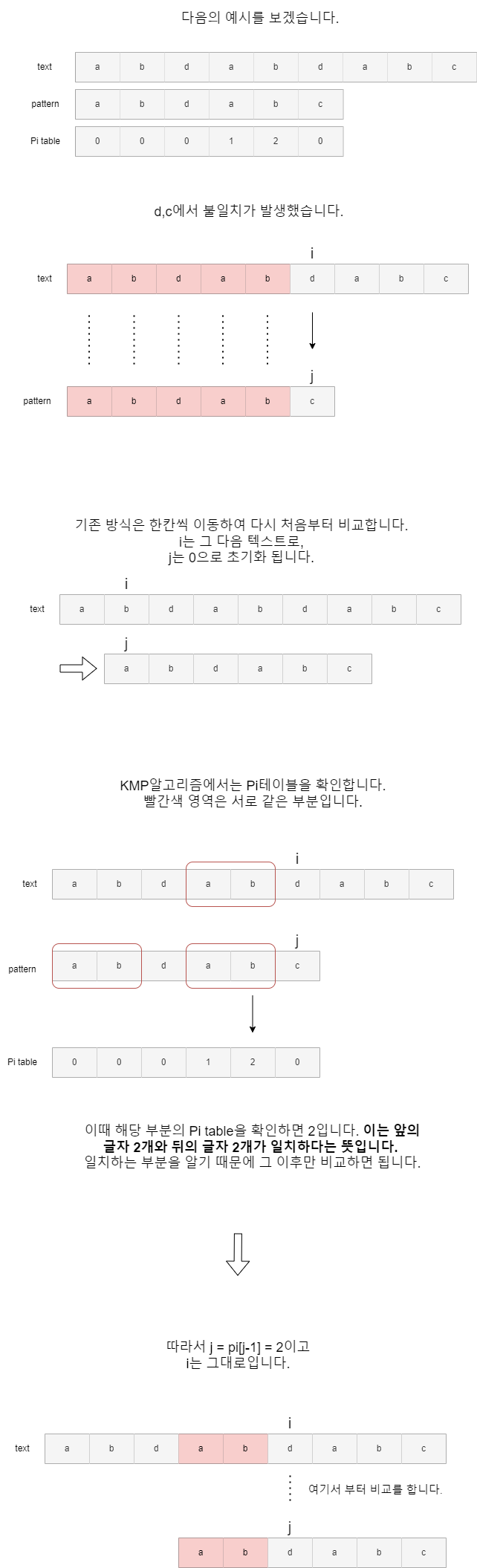
KMP 알고리즘의 시간 복잡도는 O(n + m)입니다. 여기서 n은 텍스트의 길이이고, m은 패턴의 길이입니다. 이유는 KMP 알고리즘이 Pi 테이블을 사용하여 불필요한 비교를 건너뛰고 각 문자를 한 번씩만 검사하면 되기 때문입니다. 따라서 텍스트와 패턴을 각각 한 번씩만 처리하므로 선형 시간 복잡도를 가집니다.
3) KMP알고리즘 구현
def kmp_search(text, pattern):
pi = compute_pi(pattern)
j = 0 # 패턴의 인덱스
n_text = len(text)
n_pattern = len(pattern)
found_indexes = []
# 전체 텍스트를 순회
for i in range(n_text):
while j > 0 and text[i] != pattern[j]:
j = pi[j - 1]
if text[i] == pattern[j]:
if j == n_pattern - 1:
# 패턴이 일치하는 위치를 찾음
found_indexes.append(i - j)
j = pi[j]
else:
j += 1
return found_indexes
def compute_pi(pattern):
n = len(pattern)
pi = [0] * n # 접두사 테이블 초기화
j = 0 # 접두사의 길이
# i는 1부터 문자열의 끝까지 반복
for i in range(1, n):
# j > 0이고 현재 문자가 접두사의 다음 문자와 일치하지 않는 경우
while j > 0 and pattern[i] != pattern[j]:
j = pi[j - 1] # j를 감소시키면서 일치하는 위치를 찾음 => 그다음 접두사,접미사 부분을 확인
# 현재 문자가 접두사의 다음 문자와 일치하는 경우
if pattern[i] == pattern[j]:
j += 1 # 접두사 길이를 증가
pi[i] = j # 해당 위치에 접두사 길이를 저장
return pi
string = "abdabdabc"
pattern = "abdabc"
pattern_start = kmp_search(string, pattern)
n_pattern = len(pattern)
for start in pattern_start:
end = start + n_pattern
print(string[start:end])
- 관련문제
https://www.acmicpc.net/problem/11585
'컴퓨터 > 자료구조와 알고리즘' 카테고리의 다른 글
| 자료구조와 알고리즘 - BTree구조(B-Tree, B+Tree) (0) | 2024.05.09 |
|---|---|
| 자료구조와 알고리즘 - 벡터 검색 엔진 최적화 방법: HNSW(Hierarchical Navigable Small World Graphs) (0) | 2024.05.09 |
| 자료구조와 알고리즘 - Trie (Prefix Tree) (0) | 2024.02.13 |
| 자료구조와 알고리즘 - 슬라이딩 윈도우(Sliding Window) (0) | 2024.01.02 |
| 자료구조와 알고리즘 - 투 포인터(Two Pointer) (0) | 2023.12.23 |

