
1. 배낭 문제
1)개념

배낭에 넣을 수 있는 물건 중에서
1. 배낭이 담을 수 있는 무게의 한계를 넘지 않으면서
2. 총 가치가 최대가 되는 경우를 찾는 문제입니다.
2) 배낭 문제 유형
배낭 문제는 두 개의 유형이 있습니다.
1. 분할가능(fractional)
2. 분할불가능
예시로, 금12kg의 가치를 4$라고 한다면 1kg당 1/3$의 가치를 가지게 됩니다. 이는 분할 가능한 문제입니다.
다른 예시로, 책 2kg의 가치를 10달러라고 한다면 1kg당 5달러가 될 수 있지만 현실에서 배낭에 넣을 때, 책을 찢어서 2등분으로 만든 다음에 배낭에 넣는 것은 말이 안되기 때문에 이는 분할 불가능한 문제입니다.
2. 분할가능(연속적)문제
분할 가능 문제는 다음과 같은 경우가 있습니다.

위 그림은 다이아, 금, 철광석을 채굴해서 배낭이 담을 수 있는 무게를 넘지 않으면서 최대가치를 구하는 문제입니다.
광석을들 1kg씩 채굴해서 가져 갈 수 있다고 가정하면 분할 문제가 됩니다.
- fractional(분할 가능, 연속적)문제의 해결법
- 분할 가능한 배낭문제는 가성비와 그리디 방식으로 풀 수 있습니다.
위 예시의 그림에서 다이아, 금, 철 광석의 1kg당 가성비를 구합니다.
| 다이아 | 금 | 철 | |
| 가치 | 80달러 | 90달러 | 100달러 |
| 무게 | 20kg | 30kg | 50kg |
| 1kg당 가치(가성비) | 4달러 | 3달러 | 2달러 |
그리디 알고리즘 방식처럼 지금의 상황에서 가장 높은 가성비를 가진 광석부터 채굴해서 담습니다.
1. 4달러가 가성비가 제일 높고 다이아광석은 20kg만 채굴할 수 있습니다. 따라서 남은 배낭 한계치:40-20 = 20kg,
현재 배낭에 담긴 물건의 총 가치: 4달러*20 = 80달러
2. 그 다음 가성비가 높은 것은 금 광석이고 30kg까지 채굴할 수 있습니다. 이때 남은 배낭의 한계치가 20kg이므로 20kg만 채굴해갑니다. => 현재 배낭에 담긴 물건의 총가치: 80달러 + (3달러*20) = 140달러
결론은 다이아20kg, 금20kg로, 140달러가 최대 가치입니다.
이런 방식으로 분할 문제를 풀면 항상 해(최대가치)를 보장합니다.(어떤 케이스든 항상 정답을 도출한다.)
그리고 이와 같이 분할 가능한 문제의 해를 solution(f) 라고 정의합니다.(뒤에서 분할 불가능문제를 풀때 solution(f)를 사용합니다.)
3. 분할 불가능 문제(0/1, 불연속적)
(0/1)의 의미는 물건을 (선택안함/선택함)을 의미합니다.

위 그림은 핸드폰, 노트북, 책을 선택하여 5kg를 넘지않으면서 최대 가치를 구하는 문제입니다.
모든 경우의 수(브루트 포스)를 구한다면 각 물건마다 2가지의 선택지(선택o,선택x)가 있으므로 2^3 = 8 가지의 경우의 수를 확인합니다. 이는 물건이 n개 있으면 2^n번 연산을 합니다. 따라서 모든 경우의 수로 푼다면 시간이 많이 걸리겠죠??
1) 백트랙킹
- 8가지 경우의 수를 트리로 표현하면 다음과 같이 나타낼 수 있습니다.
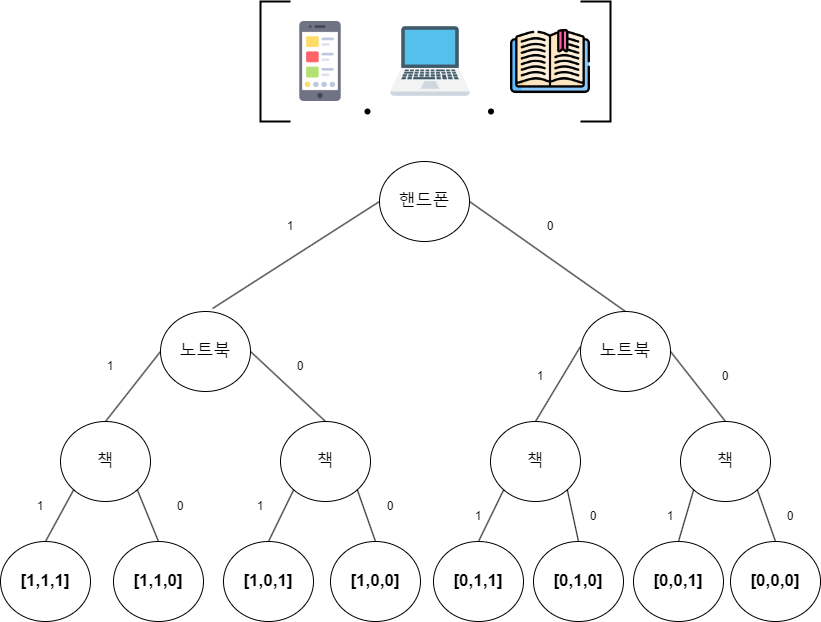
- 이때 백트랙킹의 첫번 째 조건은 선택한 물건들이 배낭의 한계치를 넘는지 검사하는 것입니다.
따라서 배낭의 한계치인 5kg을 넘는 경우는 더 이상 확인할 필요가 없습니다.

두 번째 백트랙킹의 조건은 분할 가능 문제에서의 정답인 solution(f)를 이용하는 방법입니다.
우선 위 사례에서 solution(f)를 구하면(분할 가능하다고 가정하면)
=> (5달라*3kg) + (4달러*2kg) = 23달러이다. 즉 solution(f) = 23입니다.
이번에는 위 사례를 분할 불가능이라고 가정하고 구한 해를 solution(0/1)라고 한다면 다음이 성립합니다.
solution(0/1) <= solution(f)
수학적으로 증명하지 않더라도 단순하게생각해보면
1. 분할 가능한 문제에서 solution(f)는 1kg도 남기지 않고 담고 있습니다.(가성비가 높은 순으로)
2. 반면에 분할 불가능한 문제에서는 무게를 쪼갤 수 없기 때문에 solution(0/1)은 배낭에 남는 공간이 생길 수 있습니다.
따라서 solution(0/1)은 solution(f)와 같거나 solution(f)보다 작습니다.
- 우선 왼쪽부터 탐색하여 리프노드까지 내려갑니다. 이때 21달러가 최대값이므로
solution(0/1) = 21달러로 가정합니다.(아직 확정된 거 아님)

- 그 다음 오른쪽 트리쪽을 탐색해야 하는데 바로 오른쪽 노드의 solution(f)는 19달러입니다.

- 따라서 해당 노드의 자식 노드들의 값은 항상 19달러보다 작거나 같습니다.( solution(0/1) <= solution(f) )
이는 앞서 구한 중간결과값(21달러)보다 작으므로 오른쪽 트리는 탐색할 필요가 없다.

정리하면 백트랙킹의 조건 두 가지는
1. 배낭이 담길수 있는 무게 < 선택한 물건들의 무게
2. max (중간 결과값) > 해당노드의 solution(f)
-연습 코드
weight = [3,4,2]
value = [15,16,6]
vw_ratio = [int(value[i]/weight[i]) for i in range(3)]
max_weight = 5
stack = [[0,0,-1]] # ["총무게", "가치", "레벨"]
result = []
temp_maxvalue = 0
while stack:
out = stack.pop()
total_w = out[0]
total_v = out[1]
idx = out[2]
next_idx = idx + 1
if temp_maxvalue < total_v: #중간결과값(solution(1/0)) 갱신
temp_maxvalue = total_v
if idx < 2: ## 리프노드에 도달하기 전까지
for i in range(2):
next_w = total_w + (weight[next_idx] * i)
next_v = total_v + (value[next_idx] * i)
if next_w > max_weight: #백트랙킹 1조건: 배낭한계무게 초과검사
continue
sol_f = next_v #각 노드마다 solution(f) 구하기
remain_w = max_weight - next_w
for j in range(next_idx+1, 3):
a = min(remain_w, weight[j])
sol_f += vw_ratio[j] * a
remain_w -= a
if remain_w <= 0:
break
if sol_f <= temp_maxvalue: # solution(f) <= solution(0/1) 검사
continue
stack.append([next_w, next_v, next_idx])
else: ##리프노드에 도달하면
result.append(out)
print(result)
print(temp_maxvalue)
2) DP(다이나믹 프로그래밍)
다이나믹 프로그래밍으로 문제를 풀 때는 다음의 과정으로 풉니다.
dp 배열의 의미는 다음과 같습니다.
1. dp[][]는 물건들의 총가치의 최대값
2. 첫번째 배열은 [핸드폰, 노트북,책]처럼 물건들을 선택하는 경우
3. 두 번째 배열은 무게제한

우리가 구하고자 하는 것만 dp[핸드폰, 노트북,책][5]의 값입니다.
dp[핸드폰,노트북,책][5]는
1. 책을 선택안하면 경우 => 선택을 안하므로 무게제한은 그대로이고 dp[핸드폰,노트북][5]
2. 책을 선택한 경우 => 책의 무게는 2kg이므로 dp[핸드폰, 노트북][5-2] 이고 책을 선택했으므로 +6달러를 추가합니다.
1,2의 결과 중 최대값을 dp에 저장합니다.
dp를 일반화하면 다음과 같습니다.

테이블로 표현하면 다음과 같습니다.

dp[a,b,c][5] = MAX( dp[a,b][3] + 6 , dp[a,b][5] ) = MAX (21, 16) = 21 입니다.
-연습 코드
weight = [0,3,4,2]
value = [0,15,16,6]
max_weight = 5
dp = [[0]*(max_weight+1) for _ in range(len(weight))]
for i in range(1, len(weight)):
for w in range(1, max_weight + 1):
num1 = dp[i-1][w]
if w- weight[i] < 0:
num2 = 0
else:
num2 = dp[i-1][w-weight[i]] + value[i]
dp[i][w] = max(num1, num2)
dp
-백준 배낭문제풀이
https://www.acmicpc.net/problem/12865
12865번: 평범한 배낭
첫 줄에 물품의 수 N(1 ≤ N ≤ 100)과 준서가 버틸 수 있는 무게 K(1 ≤ K ≤ 100,000)가 주어진다. 두 번째 줄부터 N개의 줄에 거쳐 각 물건의 무게 W(1 ≤ W ≤ 100,000)와 해당 물건의 가치 V(0 ≤ V ≤ 1,000)
www.acmicpc.net
import sys
n, k = [int(i) for i in sys.stdin.readline().split()]
weight = [0]
value = [0]
for _ in range(n):
w, v = [int(i) for i in sys.stdin.readline().split()]
weight.append(w)
value.append(v)
dp = [[0]*(k+1) for _ in range(n+1)]
for i in range(1,n+1):
for w in range(1,k+1):
num1 = dp[i-1][w]
if w - weight[i] < 0:
num2 = 0
else:
num2 = dp[i-1][w-weight[i]] + value[i]
dp[i][w] = max(num1, num2)
print(dp[-1][-1])
참고자료:
https://www.youtube.com/watch?v=rhda6lR5kyQ&t=762s
https://www.youtube.com/watch?v=H4UPhyhDyJk

'컴퓨터 > 자료구조와 알고리즘' 카테고리의 다른 글
| 자료구조와 알고리즘 - 유니온 파인드(Union-Find) (0) | 2023.05.04 |
|---|---|
| 자료구조와 알고리즘 - 위상정렬(Topological Sorting) (0) | 2023.04.13 |
| 자료구조와 알고리즘 - 우선순위 큐(Priority Queue)와 힙 정렬(Heap Sort) (0) | 2023.01.24 |
| 자료구조와 알고리즘 - 힙(Heap) (0) | 2023.01.21 |
| 자료구조와 알고리즘 - 그래프 (0) | 2023.01.08 |

